1. はじめに
「ラングトンのアリ」という名前を聞くと、どこか生物学的な実験や実在する生物を想像する方もいるかもしれません。
しかし、この“アリ”は実際の昆虫ではなく、コンピュータ・シミュレーションの世界で生まれた仮想的な存在です。
生物学的な意味での“アリ”ではありませんが、その振る舞いはときに生物のような複雑さ、または秩序だったパターンを示すことがあります。
セル・オートマトン(cellular automaton)の一種として研究されてきたラングトンのアリは、シンプルなルールに基づいて信じられないほど豊かな振る舞いを見せる代表的な例となっています。
コンピュータ上で動作するにもかかわらず、徐々に秩序だった動きが現れたり、ある時点から規則的な軌跡を刻むようになる様子は、まるで本物のアリが規則正しく道を作って進んでいるかのような錯覚を覚える人もいるでしょう。
ここでは、その基礎的なルールから、多彩な広がりを見せる応用例、さらには芸術・教育での活用や研究的な意味合いに至るまで、ラングトンのアリをとことん深堀りしてみようと思います。
2. ラングトンのアリとは何か

ラングトンのアリ(Langton’s ant)とは、1986年にアメリカの科学者クリス・ラングトン(Chris Langton)によって提案されたセル・オートマトンの一種です。
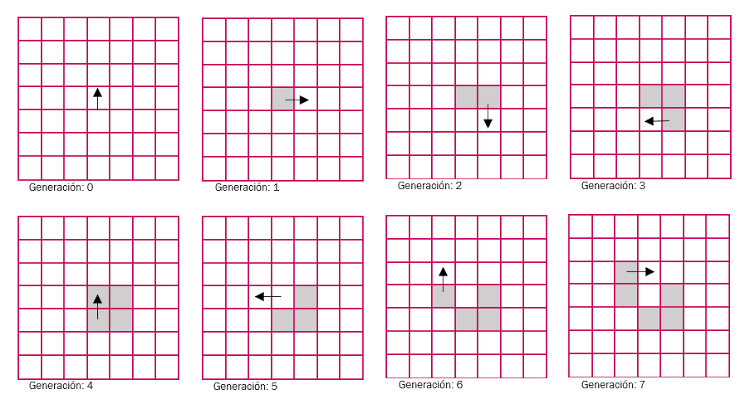
もっとも特徴的なのは、その動作を決定するルールが非常に簡単なことにあります。具体的には、無限に広がる格子状(2次元平面)のマス目の上を“アリ”が1匹だけ動いていくという単純な設定です。
- アリには「向き」がある。
- 格子状のマス目は「白(あるいは0)」か「黒(あるいは1)」の2色で塗られている。
- アリはその時にいるマス目の色によって、「左に90度回転して1マス進む」か「右に90度回転して1マス進む」を選ぶ。
- アリが通ったマス目は、色を反転(白→黒、黒→白)させる。
最初はすべてのマスが白で、アリの初期位置と初期の向きが決まっているとしましょう。そこからルールどおりに動いていくと、偶然的にも見えるパターンを生成しながら、しばらくは複雑にウロウロと動き回ります。
しかし、驚くべきことに、ある一定のステップ数を超えると、一定周期で繰り返し現れる「高速道路」的な軌跡に乗って、まるで整然とした街道の上を走るようにひたすら進み続けるようになるのです。
この不思議な現象は、セル・オートマトン研究の文脈で「創発現象」の一例として非常に有名になりました。

引用元:Langton’s Ant
3. 誕生と歴史的背景
クリス・ラングトンは、人工生命(Artificial Life)分野の研究者としても知られています。
人工生命とは、コンピュータやロボット上で、生物のような自己組織化や進化、適応などを再現しようとする学問です。
1980年代は、ジョン・ホランドの遺伝的アルゴリズムやスティーブン・ウルフラムのセル・オートマトン研究など、新しい計算モデルやシミュレーション技術を駆使して生命現象の本質を理解しようとする動きが活発だった時代でもあります。
そうした文脈の中で誕生したラングトンのアリは、当初は「単純なオートマトンが示す振る舞いの一例」として提案されました。
しかし、その後の研究やコンピュータによるシミュレーションで明らかになった、カオス的な振る舞いから秩序が生まれる現象は、多くの研究者や愛好家を魅了し続けることになります。
計算生物学や複雑系科学の一端としてだけでなく、数学パズル的な楽しさもあり、今ではプログラミング教育の題材や、アート作品のモチーフにも取り上げられるようになりました。
4. ルールの詳細
ラングトンのアリの挙動を細かく見ていくと、次のようなステップで更新されます。
- アリの現在地と現在の向きを把握する。
- 例:アリは “上” を向いており、マス(A, B) にいる。
- アリがいるマスの色を確認する。
- もしそのマスが白(0)なら、アリは左に90度回転し、次のマスに進む。
- もしそのマスが黒(1)なら、アリは右に90度回転し、次のマスに進む。
- アリが去った後のマスの色を反転させる。
- 白(0)なら黒(1)に、黒(1)なら白(0)に変更。
- 次のタイムステップに移り、再び同じルールを適用する。
シンプルすぎるほどシンプルです。初期の方向は「上」を向いているとするのが定番ですが、「右」や「左」、さらには初期位置がどのマスでも同じように挙動します。
無限の平面が前提ですが、実際のシミュレーションでは有限サイズのグリッドを用い、必要に応じて端を「巻き戻し」処理(トーラス状に結ぶ)にすることもあります。
ここまでルールが簡単だと、たとえば「すぐにループして、すべてが一定のパターンに陥ってしまうのではないか」と思われるかもしれません。
しかし実際には、しばらくのステップ数は混沌としたパターンを形成しながらも、やがて定期的に自己再生するパターン(Highway)が確立して、一定の秩序が生まれます。
この様子は、複雑系科学の代表的なキーワードである「秩序と無秩序の狭間」を象徴しているとも言えます。
5. 出現するパターンとその特徴
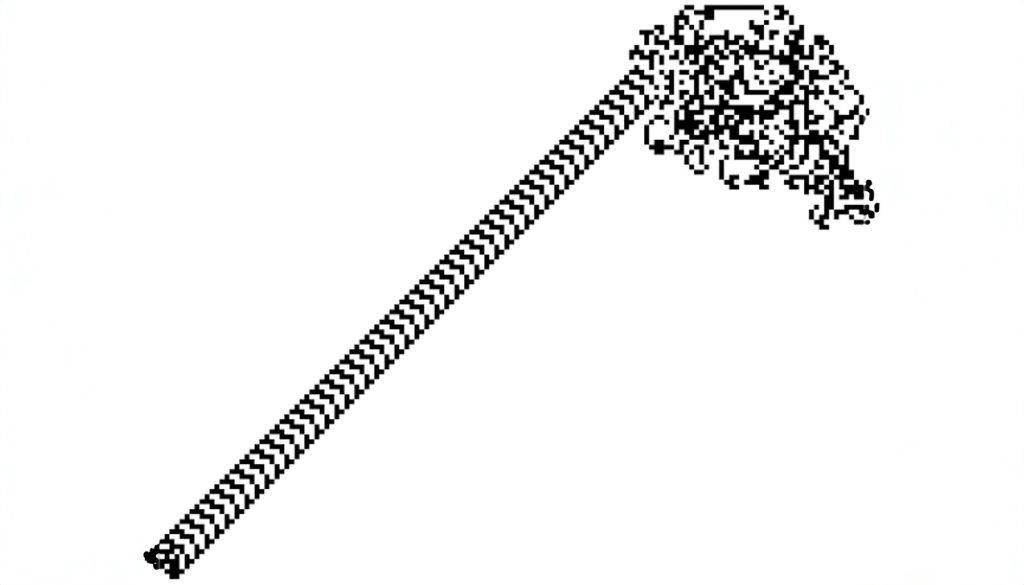
ラングトンのアリを実際にシミュレートしてみると、前半ではランダムな動きとしか思えない軌跡が描かれます。
明確な繰り返し構造が見られないため、コンピュータで初めてこのオートマトンを動かした研究者たちも「いつかはループに陥るだろう」「あるいはパターンが発散して画面いっぱいにランダムな模様を描き続けるのではないか」と予想していました。
ところがある一定のステップ数(たとえば1万ステップ前後、場合によっては1万5千ステップ付近)を超えると、アリは突如として一定の周期構造を作り始め、そこから“高速道路”のような一直線の軌跡を辿るようになります。
引用元:Langton’s Ant
この高速道路の軌跡に入ると、アリはずっとそのパターンを反復する形で、ほぼまっすぐに進んでいくようになるのです。
したがって、ラングトンのアリを観察する際には、「ランダム的な初期混沌期」と「周期的な軌跡の安定期」という2つのフェーズがあると考えてよいでしょう。
とはいえ、この「高速道路(Highway)」がいつどのように生成されるかは、初期条件や拡張ルールによって変わってきます。
面白いことに、アリの振る舞いが始まって少ないステップですぐに高速道路を作ってしまうケースもあれば、かなり長いステップ数を経ないと整然とした道ができないケースもあります。
これがランダム性と秩序の相互作用を如実に示している部分なのです。
6. “Highway” と呼ばれる特徴的な軌跡
先に触れたように、ラングトンのアリの最大の魅力は、無秩序にも見える状態から最終的に生まれる“Highway”というパターンです。
このパターンは、“対称的な形状が左右に広がっている道” というわけではありません。実際にはジグザグを繰り返すような形状で、一定の繰り返し構造によって前進し続けるのが特徴です。
具体的には、アリが「白であれば左折」「黒であれば右折」というルールに従っているため、一種の自己複製のような構造が発生しやすいのだと考えられています。

引用元:Auto-generator
自己複製といっても、コンウェイの「ライフゲーム」のグライダーなどとは異なり、ラングトンのアリではアリ自身が“複製される”のではなく、“軌跡を生成するパターン” がシフトしながら前に進む格好です。
Highwayは一旦現れると、そのパターンが壊れることはなく、ひたすら同じ周期構造を空間に刻みつづけます。
なぜこんなものが簡単なルールから自然発生するのかは完全には解明されていないものの、複雑系研究における「創発」や「自己組織化」の概念を象徴する例として頻繁に語られます。
7. なぜカオス的に見えるのか:自己組織化と秩序
ラングトンのアリが長いステップ数のあいだランダムなパターンを示すのは、セル・オートマトンという離散的なルール系が示す典型的な複雑性の一例とも言えます。
初期状態がすべて白だとしても、アリが進むうちに次第にマス目が白黒入り混じった状態になり、その状態がアリの次の行動を決定する際に“フィードバック”として働きます。
これにより、アリの軌跡は常に過去の自分自身の行動で変化してきた状態に左右され続けるため、一見するとカオス的な動きが生まれるわけです。
ところが十分に時間が経つと、一部の小さなパターンが自身のコピーのようなものを再生産しながら前進するループが確立されます。
このように、ランダムな状態から徐々に安定したパターンが出現してくるのは、まさに「自己組織化(Self-Organization)」と呼ばれるプロセスです。
自然界の多くの現象、たとえば渦巻き銀河の形成や木の葉脈のパターン、脳内の神経ネットワークの配線などでも、局所的なルールから秩序だった構造が現れる例が数多く観察されます。
ラングトンのアリは、その自己組織化の基本的なメカニズムを理解するための手軽な教材としても活用されています。
8. Pythonによる簡単な実装例
ここで、実際にラングトンのアリをプログラムで実装する方法を簡単に紹介します。Pythonを使った例を示しますが、他の言語でも同様のロジックで動作します。
import matplotlib.pyplot as plt
import numpy as np
# グリッドサイズ(シミュレーションを切り取る範囲)
GRID_SIZE = 200
# マス目を0で初期化(すべて白)
grid = np.zeros((GRID_SIZE, GRID_SIZE), dtype=int)
# アリの初期位置
x = GRID_SIZE // 2
y = GRID_SIZE // 2
# 方向を表す(上:0, 右:1, 下:2, 左:3)
direction = 0
# シミュレーションステップ数
steps = 11000
# 各ステップのアリの位置を記録して可視化
x_positions = []
y_positions = []
for _ in range(steps):
x_positions.append(x)
y_positions.append(y)
if grid[y, x] == 0:
# 白なら左回転
direction = (direction - 1) % 4
grid[y, x] = 1
else:
# 黒なら右回転
direction = (direction + 1) % 4
grid[y, x] = 0
# 方向に応じて前進
if direction == 0: # 上
y -= 1
elif direction == 1: # 右
x += 1
elif direction == 2: # 下
y += 1
elif direction == 3: # 左
x -= 1
# 範囲外に出そうになったら折り返し(あるいは無視)
x = x % GRID_SIZE
y = y % GRID_SIZE
# 最後の状態を可視化
plt.figure(figsize=(8, 8))
plt.imshow(grid, cmap='binary')
plt.title(f"Langton's Ant after {steps} steps")
plt.show()
このプログラムでは、以下のような点が重要になります。
gridという2次元配列でマス目を管理しており、0を白、1を黒として区別している。directionは 0,1,2,3 の4つで上下左右を表している。- マスの色に応じて左回転か右回転かを決め、現在いるマスの色を反転させた後、一マス前進する。
- 端を越えたら
x = x % GRID_SIZEで反対側にループさせている(トーラス状の空間になる)。
ステップ数を増やしてシミュレーションすると、初期はランダムに動き回るように見えるアリが、数千ステップを超えたあたりで徐々に「高速道路」を作り始めるのが観察できるでしょう。
ステップ数が1万を超えると、ほとんど安定して高速道路を進んでいる姿が見えるはずです。
9. 変形・拡張モデル
ラングトンのアリは、もともと「白であれば左折、黒であれば右折」という一種類のアリを想定していました。
しかし、その後の研究・愛好家たちの遊び心によって、様々なバリエーションが提案されています。
主なものをいくつか紹介します。
- ターンの角度を変える
- 90度ではなく、例えば120度や60度など他の角度で回転するバージョンがあります。六角形格子(hexagonal grid)を使う場合などに応用されることもあります。
- 色の数を増やす
- 2色だけでなく、3色、4色、あるいはそれ以上の色を持つマスとルールを設定する拡張です。色ごとにアリがどちらへ回転するかを決めたり、あるいはアリのスピードや振る舞い自体を色によって変化させたりします。
- 複数のアリを同時に走らせる
- 複数のアリが同じ平面で動くとき、それぞれが独立してマスの色を反転させます。アリ同士が衝突(同じマスに来る)した時のルールをどうするかなど、さまざまな面白い問題が発生します。
- 遺伝的アルゴリズムとの組み合わせ
- 初期条件や回転方向のルールを進化的に更新していく、いわゆる「進化するアリ」のモデル。特定の目的(たとえばグリッド全体を黒にするなど)を達成するためにルールを最適化する実験なども行われています。
こうした拡張モデルは、既存のラングトンのアリが示す不思議な創発現象をさらに一般化したり、異なるパターンの“Highway”が見られることを示したりと、研究・趣味の両面で面白い題材となっています。
10. 他のセル・オートマトンとの比較
ラングトンのアリは、多くのセル・オートマトンの中でも特に有名な存在ですが、代表的な他のセル・オートマトンとしては「ライフゲーム(Conway’s Game of Life)」や、スティーブン・ウルフラムによる1次元セル・オートマトン(ルール110やルール30など)が挙げられます。
- ライフゲーム
ライフゲームは2次元平面で、各セルが「生」か「死」のどちらかにあり、隣接セルの数に応じて次の状態が決まるルールです。
非常に単純なルールでありながら、無限に増殖するパターンや周期的なオシレーター、自己移動するグライダーなど、多彩な現象が見られます。
ラングトンのアリとの大きな違いは、ライフゲームでは複数のセルが同時並行的に状態を更新するのに対し、ラングトンのアリは基本的に「アリ1匹の動き」に焦点を当てている点です。 - 1次元セル・オートマトン(ルール30、ルール110など)
これは一列のセルに対して、隣接セル3つの状態を元に自分の次の状態を決める仕組みです。
ルール30で生成されるパターンは見かけ上ランダムに近く、乱数生成器としての性質が研究されています。
一方、ルール110ではチューリング完全であることが証明されており、簡単なルールから複雑な計算能力が生まれることを示す代表例です。
ラングトンのアリも、拡張ルール下ではチューリング完全であるという議論があります。 - その他の2次元オートマトン
たとえばBrian’s BrainやWireWorldなど、多種多様なルールが存在します。
いずれも、局所的なルールが思わぬ複雑さや秩序を生み出す例として面白い研究対象です。
ラングトンのアリは一見するとライフゲームほどの“細胞数の同時更新”によるダイナミズムは感じられないかもしれません。
しかし、単一のエージェント(アリ)と2色のセルという極限までシンプルな構造でありながら、自己組織化とカオスがダイナミックに展開していく様子は、他の多くのオートマトンと同等か、あるいはそれ以上の興味深さを持っています。
11. 芸術・教育・研究分野への応用
芸術的応用
ラングトンのアリが描く軌跡は、初期の混沌期においてはランダムな模様が、安定期においては繰り返し模様が混在し、視覚的に非常に魅力的です。こうしたグラフィックパターンをアート作品に仕立てる動きもあります。
- 高速道路を可視化してアートパネルにしたり、3Dプリンタを使って軌跡を立体化して飾ったりという試みがあります。
- 音楽や映像と組み合わせて、インタラクティブなインスタレーションに活用されることもあります。
教育的応用
プログラミング教育の分野では、ラングトンのアリは「ルールがシンプルで実装が容易、かつ結果が視覚的に面白い」ため、初学者向けの教材にしばしば使われます。特に、以下のような教育的意義があります。
- 配列操作やモジュール化の学習
- 2次元配列の操作、ルールの実装、可視化など多くの基礎的技術が学べる。
- 状態遷移の概念の理解
- 「白なら左折・黒なら右折」といった条件分岐や状態反転が明確で、初学者でも理解しやすい。
- 創発現象の導入
- 少数のルールから複雑なパターンが生まれることを実感でき、複雑系やアルゴリズム思考への入り口として最適。
研究的応用
ラングトンのアリ自体がもつ計算能力や、拡張したバリエーションにおいてはチューリング完全性を持つ可能性が議論されています。
実際にこのアリを基盤として、以下のような研究テーマが挙げられます。
- 計算理論との関連: 特定の初期条件を与え、ある局所的な計算をラングトンのアリの軌跡で実装できるかといった問題。
- 自己組織化現象の数理解析: ランダムな初期条件からいかにしてHighwayが生成されるのか、その確率的・統計的アプローチ。
- 多エージェントシステムとの類似性: 複数のアリを導入したとき、群れとしての秩序が生まれるかどうかを調べる。アントコロニー最適化などのアルゴリズム研究とも関連が深い。
12. まとめと今後の展望
ラングトンのアリは、わずか「白と黒のマス」と「左折・右折」というルールだけで構成された非常にミニマルなセル・オートマトンです。
しかし、その見かけの単純さに反して、十分に長いステップを経ると突然秩序だった“Highway”が現れるという魅力的な挙動を示します。
これは複雑系科学における「創発」の代表例であり、カオスから秩序が生まれるプロセスを手軽に観察することができます。
このようにラングトンのアリには、教育的・芸術的・研究的な価値が多分に含まれています。例えばプログラミングを学ぶ入り口としては、シンプルかつビジュアルの変化が大きい題材として最適です。
また、複雑系やセル・オートマトンに興味を持つ人にとっても、ライフゲームや他の有名なルールとの比較を通じて新たな発見や理解を深める手掛かりになるでしょう。
さらに、今後は機械学習や進化計算と組み合わせて、ラングトンのアリやその拡張モデルを「学習させる」ことで、より興味深いパターン生成や、特定のタスクを解くような“自律エージェント”に仕立てる研究が進む可能性もあります。
もともと人工生命の分野から生まれた背景を考えると、コンピュータ科学と生物学のあいだの接点に位置する豊かなトピックと言えるでしょう。
セル・オートマトンは、まだまだ未知の可能性を秘めた研究分野です。ラングトンのアリもその一角として、シンプルで美しいルールの奥底に、いまだ見ぬ驚くべき世界を隠しているかもしれません。
一度プログラムを動かしてみて、カオスから秩序へ移り変わる“一瞬”をスクリーン上で観察してみると、その奥深さに心惹かれることでしょう。
ぜひ興味を持たれた方は、実装をカスタマイズしたり、複数のアリを走らせたり、色数を増やしたりと、自由な発想で遊んでみることをおすすめします。
最後に
以上が、ラングトンのアリについての詳細な解説でした。
単純なルールにもかかわらず、膨大なステップを進んだ先に出現する秩序立ったパターンは、多くの人々を惹きつける魅力を持っています。
プログラミングを通して体感するのはもちろん、美術作品や学術研究など、多方面で活用や発展が見込まれています。
ぜひ、このブログ記事をきっかけに、ラングトンのアリの世界へ踏み込んでみてください。
1匹のアリが描く軌跡をじっと眺めていると、あなた自身も「意外と世界はシンプルなルールから複雑なものが生まれているのかもしれない」と思えてくるかもしれません。
そうした気づきこそ、ラングトンのアリが私たちにもたらしてくれる大きな恩恵の一つなのです。


コメント